La notation MMSTD (Mills Mess State Transition Diagram)
Article proposé par Frédéric Roudaut.
Le 24/03/2007.
SOMMAIRE
III – LA NOTATION MMSTD DANS SA FORME SIMPLE
1 – Position des bras dans la notation MMSTD
4 – Le State Transition Diagram – l’exemple du Windmill
5 – Le State Transition Diagram en format texte
6 – Les transitions naturelles du State Transition Diagram
IV - INTEGRATION DU SITESWAP DANS LA NOTATION MMSTD
1 – Le State Transition Diagram avec siteswaps
V - LES LIMITES DE LA NOTATION MMSTD
1 – Le diagramme MMSTD et l'algorithmique des graphes
2 – Génération de tous les patterns valides en Python
I - AVANT DE COMMENCER
On trouve à l’heure actuelle sur le Net un certain nombre de documents relatifs à la notation MMSTD. Ce document a pour principal objectif de synthétiser ces différents éléments et d’aider les non anglophones à comprendre la notation MMSTD ;-) . Peut-être qu’ainsi certains d’entre vous contribueront à repousser encore les limites de cette notation qui je vous rassure n’a strictement rien de mathématique ;-).
La fin de cet article présente un petit outil tentant de donner une nouvelle ouverture à cette notation par la présentation des différents patterns rendus possibles.
Cet article sera suivi d'un autre relatif à l'application de la notation MMSTD sur la notation S,O,U. Par conséquent, vous trouverez au-besoin de nombreux exemples supplémentaires dans le dit document.
II – INTRODUCTION
La notation MMSTD est une notation inventée par Mike Day (un des co-développeur de la notation Siteswap) pour préciser les mouvements de mains de certains patterns de jonglerie. La notation Siteswap prend en effet en compte le timing mais ne s’intéresse pas aux mouvements des mains (Pour de plus amples renseignements concernant la notation Siteswap référez-vous à l’article correspondant dans la rubrique Théorie).
La notation MMSTD a été originellement définie afin d’analyser, de comprendre et de manipuler la figure bien connue baptisée Mill’s Mess. MMSTD est l’abréviation de Mills Mess State Transition Diagram. Nous verrons par la suite ce que sont ces diagrammes de transition d’état.
Avant tout, il faut préciser que la notation MMSTD ne couvre pas l’intégralité des mouvements possibles. Cependant, elle permet de décrire et d’analyser certains patterns, d’en déduire d’autres. Par la suite nous verrons qu’avec quelques limitations (notamment sur les multiplexes et les lancers synchrones) nous pouvons incorporer les Siteswaps dans la notation MMSTD.
III – LA NOTATION MMSTD DANS SA FORME SIMPLE
Contrairement à la notation Siteswap qui prend en compte le timing, la notation MMSTD s’intéresse à ce que l’on va qualifier de beat un peu à la manière d’une partition musicale . Chaque beat est l’enchaînement d’un lancer suivi d’une rattrape. Le temps entre les deux pouvant être assez long, on fait néanmoins l’hypothèse que ces échanges sont simultanés. L’hypothèse majeure de la notation concerne la succession des mouvements Main Droite/Main Gauche. Forcément, basé sur ces simples hypothèses on exclut les lancers multiplexes ainsi que les lancers synchrones.
Ce chapitre ne prendra pas en compte les siteswaps. La notation MMSTD sera explicitée dans sa forme la plus simple sans prendre en compte les siteswaps.
1 – Position des bras dans la notation MMSTD
La notation se restreint à 3 positions possibles pour les bras. Soit les bras sont décroisés, soit les bras sont croisés, bras droit dessus ou dessous.
2 – Les échanges
La notation MMSTD utilisant donc uniquement les mouvements des bras; intéressons-nous aux différents échanges que l’on peut rencontrer.
Considérons 2 balles, une dans la main droite, une dans la gauche. La main gauche effectue le premier lancer. Si l’on considère maintenant la main droite, vous pouvez effectuer un lancer bras décroisés et attraper la balle précédente avec une rotation horaire ou anti-horaire vue du jongleur. Dans le cas d’une rotation horaire, on parle d’Inside Exchange, dans le cas d’une rotation anti-horaire on parle d’Outside Exchange.
Maintenant, prenons le cas où vos bras sont croisés, bras droit au-dessus de bras gauche ou inversement. Votre main droite doit lancer une balle avant d’attrapez la précédente. On utilise toujours les mêmes dénominations, à savoir on parle d’Inside Exchange dans le cas d’une rotation horaire et dans le cas d’une rotation anti-horaire on parle d’Outside Exchange.
Si l’on inverse maintenant les lancers, à savoir la main droite effectue le premier lancer, la main gauche le second avant d’attraper la première balle. On se retrouve donc dans une figure symétrique. Lorsque les bras sont décroisés, dans le cas d’une rotation anti-horaire, on parle d’Inside Exchange, dans le cas d’une rotation horaire on parle d’Outside Exchange.
Et de même, prenons le cas où vos bras sont croisés, bras droit au-dessus de bras gauche ou inversement. Votre main gauche doit lancer une balle avant d’attrapez la précédente. On utilise toujours les mêmes dénominations, à savoir on parle d’Inside Exchange dans le cas d’une rotation anti-horaire et dans le cas d’une rotation horaire on parle d’Outside Exchange.
Les figures suivantes illustrent ces différents échanges. Vous noterez bien que dans la notation MMSTD on s’intéresse aux échanges plutôt qu’aux trajectoires suivies par les balles.
Inside Exchanges :
La vidéo suivante présente de gauche à droite :
- un Inside Exchange de la main droite
- un Inside Exchange de la main gauche.
La vidéo suivante présente de gauche à droite et de haut en bas:
- un Inside Exchange de la main droite, bras droit au-dessus.
- un Inside Exchange de la main gauche, bras gauche au dessus.
- un Inside Exchange de la main droite, bras gauche au dessus.
- un Inside Exchange de la main gauche, bras droit au-dessus.
Outside Exchanges :
La vidéo suivante présente de gauche à droite :
- un Outside Exchange de la main droite.
- un Outside Exchange de la main gauche.
La vidéo suivante présente de gauche à droite et de haut en bas:
- un Outside Exchange de la main droite, bras droit au-dessus.
- un Outside Exchange de la main gauche, bras gauche au dessus.
- un Outside Exchange de la main droite, bras gauche au dessus.
- un Outside Exchange de la main gauche, bras droit au-dessus.
Par simplicité vous pouvez juste retenir que :
|
3 – Les états
A chaque échange on va associer un état dépendant de la main qui lance et de la position des bras. Cet échange est noté :

Où X prend les valeurs :
- U : lorsque les bras sont décroisés
- L : lorsque le bras gauche est positionné au dessus du bras droit
- R : lorsque le bras droit est positionné au dessus du bras gauche
Et y prend les valeurs :
- l : lorsque le bras gauche lance la balle
- r : lorsque le bras droit lance la balle
Si l’on reprend les vidéos précédentes, on comprend maintenant les indications Ur, Ul, Rr, Ll, Lr, Rl pour les Inside Exchanges ainsi que pour les Outside Exchanges.
Ces états sont les seuls disponibles avec la notation MMSTD. Vous constaterez donc que l’on se retrouve limité pour la description de certaines figures. En particulier si les mouvements ne modifient pas la position des mains, les états resteront identiques.
Etats U (Uncrossed) :
La vidéo suivante présente de nouveau les différents états U. En partant de gauche à droite et de haut en bas on a :
- Ur avec un Inside Exchange.
- Ur avec un Outside Exchange.
- Ul avec un Inside Exchange.
- Ul avec un Outside Exchange.
Etats R (Right Over) :
La vidéo suivante présente de nouveau les différents états R. En partant de gauche à droite et de haut en bas on a :
- Rr avec un Inside Exchange.
- Rr avec un Outside Exchange.
- Rl avec un Inside Exchange.
- Rl avec un Outside Exchange.
Etats L (Left Over) :
La vidéo suivante présente de nouveau les différents états L. En partant de gauche à droite et de haut en bas on a :
- Lr avec un Inside Exchange.
- Lr avec un Outside Exchange.
- Ll avec un Inside Exchange.
- Ll avec un Outside Exchange.
Pour résumer les états disponibles sont :
|
4 – Le State Transition Diagram – l’exemple du Windmill
Maintenant que nous disposons des états, il s’agit de définir les transitions entre ces états pour obtenir le State Transition Diagram. Les transitions ne sont ni plus ni moins que les échanges. On notera I sur les transitions pour les Inside Exchanges et O pour les Outside Exchanges.
Le Windmill (Moulin à Vent) est un bon exemple pour illustrer ces différents principes et construire vos premiers State Transition Diagrams. Les vidéos suivantes illustrent deux manières différentes d’exécuter le Windmill. Vous pouvez choisir de récupérer les balles soit par dessus votre bras opposé, soit par dessous.
Windmill Variante n°1 (récupération par Dessous)
Windmill Variante n°2 (récupération par Dessus)
Intéressons nous dans un premier temps à la vidéo Windmill n°1 dans laquelle les récupérations de la main droite sont toujours effectuées par dessous le bras gauche. Si l’on s’intéresse aux états on constate que l’on a une succession des états Ll, Ur. En effet les lancers main gauche sont toujours effectués bras gauche au-dessus ; les lancers main droite sont toujours effectués bras décroisés.
Pour ce qui est des transitions, il vous suffit de visualiser les mains lors des rattrapes. Les mains droite et gauche récupèrent toujours la balle dans un mouvement anti-horaire (à la gauche du lancer, vu du jongleur). On obtient donc un Inside Exchange pour la main gauche et un Outside Exchange pour la main droite.
Tout naturellement, il en découle le diagramme suivant :

Que l’on lit littéralement par :
- Bras gauche au-dessus, lancez main gauche et attrapez la balle précédente (de main droite) dans un mouvement anti-horaire ou Inside Exchange.
- Bras décroisés, lancez main droite et attrapez la balle précédente (de main gauche) dans un mouvement anti-horaire ou Outside Exchange
Le diagramme de la vidéo Windmill n°2 est sensiblement le même. Les transitions sont similaires. La différence étant que cette fois-ci le bras gauche passe par dessous le bras droit et non plus par dessus. On se rend donc compte que la seule différence réside dans l’état Ll qui cette fois-ci devient Rl. On en déduit le diagramme suivant :

5 – Le State Transition Diagram en format texte
Bien entendu, dessiner de tels diagrammes est un inconvénient. Textuellement on peut donc tout simplement écrire :
Pour la vidéo Windmill n°1 :
----+---> Ur
Ll <---o---
Pour la vidéo Windmill n°2 :
----+---> Ur
Rl <---o---
Le + remplaçant le I et o remplaçant le O du diagramme pour des questions de limites des caractères ASCII.
6 – Les transitions naturelles du State Transition Diagram
Nous ne démontrerons pas les transitions. Voici les transitions les plus naturelles telles que définies par Mike Day :

Ce diagramme vous aidera à dériver d’autres figures à partir du diagramme d’une figure.
Les transitions absentes ne signifient en aucun cas qu’elles sont impossibles mais simplement qu’elles sont considérées comme étant moins naturelles.
Ces transitions considérées comme non naturelles sont donc :
Ll -o-> Ur Ll -o+-> Ul Ll -o+-> Rl Ll -o+-> Rr |
Ur -+-> Ll Ur -+-> Rl Ur -o+-> Rr Ur -o+-> Lr |
Rl -o-> Ur Rl -o+-> Ul Rl -o+-> Ll Rl -o+-> Lr |
Rr -o-> Ul Rr -o+-> Ur Rr -o+-> Ll Rr -o+-> Lr |
Ul -+-> Lr Ul -+-> Rr Ul -o+-> Ll Ul -o+-> Rl |
Lr -o-> Ul Lr -o+-> Ur Lr -o+-> Rl Lr -o+-> Rr |
Ce qui nous donne le diagramme suivant pour les transitions non naturelles :
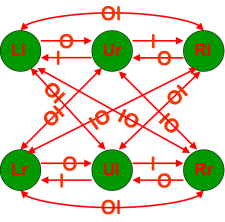
7 – Les Symétries
Déduire la symétrie d'un diagramme MMSTD est relativement aisée. Sans aucune explication vous comprendrez qu'il suffit de transformer les R en l et inversement pour les différents états du diagramme.
On a ainsi le tableau de correspondances suivants pour les symétries :
Rr |
Ll |
Ll |
Rr |
Ur |
Ul |
Ul |
Ur |
Rl |
Lr |
Lr |
Rl |
Si on applique ce principe au Windmill n°1 de diagramme :
 |
---+---> Ur |
on obtient le diagramme suivant :
<---o--- Ul |
8 – Les Inversions dans le temps (Time Reversed)
De tels diagrammes peuvent nous permettre de dériver des figures inversées dans le temps. Une figure inversée est une figure que l’on obtiendrait par simple visionnage à l’envers de la vidéo d’une figure en question. On parle de Time Reversed en anglais.
Sans autre démonstration on constatera simplement que dans le cas d’une figure Time Reversed:
- les lancers deviennent des rattrapes et inversement.
- La séquence des événements est inversée.
- les Outsides Exchanges deviennent des Insides Exchanges et inversement les Insides Exchanges deviennent des Ousides Exchanges.
Pour obtenir le diagramme sans siteswap d’une figure Time Reversed il suffit donc :
|
Si on applique ce principe au Windmill n°1 de diagramme :
 |
---+---> Ur Ll <---o--- |
on obtient le diagramme suivant :
 |
<---o--- Ul Lr ---+---> |
Par simple inversion de la vidéo, on peut vérifier ce diagramme :
De la même manière si on applique ce principe au Windmill n°2 de diagramme :
| ---+----> Ur Rl <---o---- |
on obtient le diagramme suivant :
| <----o--- Ul Rr ----+---> |
Par simple inversion de la vidéo, on peut également vérifier ce diagramme :
9 – Utilisation de la notation pour trouver des transitions
La notation MMSTD peut également vous permettre de trouver des transitions entre vos figures. Il vous suffit simplement d'écrire les notations MMSTD de vos figures puis de les composer en utilisant le diagramme des transitions valides. Essayons ainsi de composer un Half Boston Mess avec un Funky Mess ou encore un Mill's Mess.
Avant de commencer précisons la notation S, O, U. Pour décrire un lancer, on peut utiliser la notation S, O, U avec :
- O = Over pour un lancer au-dessus du bras.
- S = Side pour un lancer normal bras décroisés.
- U = Under pour un lancer sous le bras opposé.
Si on reporte ces différentes lettres sur le diagramme des transitions valides on obtient :

Vous constatez donc que la granularité de la notation MMSTD est plus fine que celle de la notation S, O, U. La notation S, O, U ne permet pas de définir des relations entre les différents états mais elle nous aidera dans la visualisation des diagrammes d'états présentés par la suite.
Voici en vidéo une des variantes du Half Boston Mess notée (Var. 1) :
Vous constaterez qu'ici les balles sont lancées en colonne et la balle du milieu est lancée tantôt par la main gauche, bras décroisés, tantôt par la main droite, bras gauche au dessus.
Le diagramme MMSTD associé est le suivant :
Ll -+-> Lr -+-> Ul -+-> Ur -o-> Ul -o-> Lr -o-> Ll [OUSSSU]
qui est équivalent à :
Lr -+-> Ul -+-> Ur -o-> Ul -o-> Lr -o-> Ll -+-> Lr [USSSUO] (Var. 1)
De la simple définition du Half boston Mess on en déduit les variantes suivantes :
- Var. 2: La balle du milieu est lancée tantôt par la main droite, bras décroisés, tantôt par la main gauche, bras droit au dessus. Il s'agit en fait de la symétrie de Var 1. Le diagramme MMSTD associé est le suivant :
Rr -+-> Rl -+-> Ur -+-> Ul -o-> Ur -o-> Rl -o-> Rr [OUSSSU]
ou encore en réorganisant :
Rl -+-> Ur -+-> Ul -o-> Ur -o-> Rl -o-> Rr -+-> Rl [USSSUO] (var. 2)
- Var. 3: La balle du milieu est lancée tantôt par la main droite, bras décroisés, tantôt par la main gauche, bras gauche au dessus. Le diagramme MMSTD associé est le suivant
:
Ur -o-> Ll -o-> Lr -+-> Ll -+-> Ur -+-> Ul -o-> Ur [SOUOSS]
- Var. 4: La balle du milieu est lancée tantôt par la main gauche, bras décroisés, tantôt par la main droite, bras droit au dessus. Il s'agit en fait de la symétrie de Var 3. Le diagramme MMSTD associé est le suivant :
Ul -o-> Rr -o-> Rl -+-> Rr -+-> Ul -+-> Ur -o-> Ul [SOUOSS]
ou encore en réorganisant :
Rr -+-> Ul -+-> Ur -o-> Ul -o-> Rr -o-> Rl -+-> Rr [OSSSOU] (var. 4)
ou encore en réorganisant :
Ll -+-> Ur -+-> Ul -o-> Ur -o-> Ll -o-> Lr -+-> Ll [OSSSOU] (var. 3)
Avant tout, voici en vidéo le Funky Mess :
Le Funky Mess a pour diagramme :
Rr -+-> Rl -+-> Ur -o-> Ll -+-> Lr -+-> Ul -o-> Rr [OUSOUS]
En combinant ce funky Mess avec les deux variantes de Half Boston Mess suivantes:
Lr -+-> Ul -+-> Ur -o-> Ul -o-> Lr -o-> Ll -+-> Lr [USSSUO] (Var. 1)
Rl -+-> Ur -+-> Ul -o-> Ur -o-> Rl -o-> Rr -+-> Rl [USSSUO] (Var. 2)
de la manière suivante :

Voici donc en vidéo la figure associée :
On aurait aussi bien pu découper le Funky Mess en deux figures SOU en y intégrant les Var.1 et Var.2 du Half Boston Mess vues en SSSUOU ou encore en SUOUSS.
On aurait également pu découper le Funky Mess comme présenté ci-dessous en deux OUS pour y intégrer les deux Halfs Boston Mess vues en OUSSSU :

Le mouvement de rotation des balles étant dans le séquencement USO, il me semblait préférable visuellement de découper le Funky Mess en 2 figures USO.
On aurait obtenu d'autres figures légérement différentes en considérant les variantes 3 et 4.
Mill’s Mess / Half Boston Mess
Avant tout, voici en vidéo le Mill's Mess :
Le Mill's Mess a pour diagramme :
Ur -o-> Rl -+-> Rr -+-> Ul -o-> Lr -+-> Ll -+-> Ur [SUOSUO]
En combinant le Mill's Mess avec les deux variantes de Half Boston Mess suivantes:
Ll -+-> Ur -+-> Ul -o-> Ur -o-> Ll -o-> Lr -+-> Ll [OSSSOU] (Var. 3)
Rr -+-> Ul -+-> Ur -o-> Ul -o-> Rr -o-> Rl -+-> Rr [OSSSOU] (Var. 4)
de la manière suivante :

Voici donc en vidéo la figure associée :
On aurait aussi bien pu découper le Mill's Mess en deux figures SUO pour y intégrer les deux Halfs Boston Mess vues en SSSOUO ou encore en SOUOSS, mais le mouvement de rotation des balles étant dans le séquencement OSU, il me semblait préférable visuellement de découper le Mill's Mess en 2 figures OSU.
On aurait obtenu d'autres figures figures légérement différentes en considérant les variantes 1 et 2.
IV - INTEGRATION DU SITESWAP DANS LA NOTATION MMSTD
Je conseille vivement aux lecteurs qui ne connaissent pas la notation siteswap de se rendre dans l'onglet Théorie pour y remédier rapidement afin de faciliter la compréhension de la suite ;-)
1 - Le State Transition Diagram avec siteswaps
Voici une vidéo d'une figure de siteswap 42 baptisée Infinite Loop :
Vous constaterez que la main droite porte une balle. On n'a donc pas véritablement d'échanges ici avec la main droite. On convient cependant de nommer Inside Exchange lorsque la balle est portée vers l'extérieur de la figure et Outside Exchange lorsque celle-ci est portée vers l'intérieur de la figure. De ces dénominations on en déduit le diagramme suivant:

Ce diagramme est simplement un pattern, c'est à dire qu'il indique la position des bras ainsi que les exchanges. Bien que donnant des indications sur les lancers, Il n'indique en aucun cas comment sont lancées les balles, ni de quelle figure il s'agit.
Pour preuve, chercher le diagramme de la figure suivante :
Vous constaterez que ces deux figures complétement différentes ont cependant le même diagramme. Comment les différencier alors ? Simplement par adjonction des siteswaps. Sur chaque état il suffit d'ajouter la valeur associée. L'Infinite Loop, décrit par le siteswap 42 aura donc le diagramme suivant :
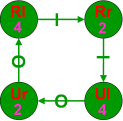
Notre dernière vidéo quand à elle est décrite par le siteswap 3. Elle donnera le diagramme suivant :

Pour un pattern donné on peut donc dériver différentes figures simplement en utilisant différents siteswaps. C'est le cas des différents Mill's Mess 531, 441 ...
Essayez donc de jongler un 51 sur le pattern précédent ou mieux encore, avec 4 balles un 44, 53 ... La période du siteswap n'étant pas forcément alignée sur le nombre d'états, vous pouvez également jongler un 633 sur le pattern précédent.
2 - Simplifications de la notation
La notation MMSTD peut être grandement simplifiée. Si l’on se rappelle du diagramme de la figure baptisée Infinite Loop on avait :
... -+-> Ul -o-> Ur -o-> Rl -+-> Rr -+-> Ul -o-> ...
4 2 4 2 4
Les états alternant les mains, il n’est pas forcément utile de les conserver. Il suffit de se rappeler la main du premier état. On obtient donc le diagramme temporaire suivant :
(l) [r] [l] [r] [l]
... -+-> U -o-> U -o-> R -+-> R -+-> U -o-> ...
4 2 4 2 4
Les mains des états sont temporairement conservées entre crochets et déduites du premier lancer (l). Sans autre simplification, il est impossible de supprimer la main du premier lancer (l) puisque les états prennent toujours en compte les mains.
Néanmoins cette restriction n’est pas vraiment importante. L’important n’est pas de savoir quelle est la main au-dessus ou au dessous mais de savoir si la main qui lance va passer au dessus ou au-dessous de l’autre. Si on note A (Above) lorsque la main passe au dessus de l’autre après le lancer et B (Below) lorsqu’elle passe dessous on peut supprimer cette restriction. Le diagramme suivant présente les cas d'utilisation de ces 2 lettres :
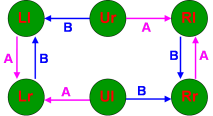
En ajoutant ces lettres aux diagrammes précédents on obtient:
(l) [r] [l] [r] [l]
... -+-> U -o-> U -o-> R -+-> R -+-> U -o-> ...
4 2 A 4 B 2 4
De ce diagramme on peut donc totalement supprimer L, U et R :
... -+-> 4 -o-> 2A -o-> 4B -+-> 2 -+-> 4 -o-> ...
Dans le document originel sur MMSTD, Mike Day établit pour convention que les échanges sont par défaut des Inside Exchanges. Si ceux-ci sont des Outside Exchanges il convient de placer une barre horizontale au-dessus du siteswap. Ce qui nous donnerait le diagramme suivant :
_ _
4 2 4 2
A B
Cette notation est relativement intéressante mais Mike Day la considère comme problématique à cause de son écriture sur deux lignes avec des barres horizontales. En effet, il vaut mieux la modifier légèrement même si l’on perd en lisibilité afin de l’adapter à des outils informatiques de génération automatique. Il convient donc de la modifier en plaçant "i" ou "o" ainsi que A, B et U après chaque nombre. On obtient donc la forme suivante :
4oU 2oA 4iB 2iU
Evidemment, le diagramme sera le même pour l’Infinite Loop commençant par la main droite et sa symétrie débutant par la main gauche. Mais cela n’a pas forcément d’importance.
Voici donc quelques exemples de figures :
Figure |
Nombres d'objets
|
Notation |
| Alternating Weave | 3 |
4oU 2oA 5iB 2iU 2iU |
| Burke's Barrage | 3 |
4iB 2iU 3oA |
| Cascade | X |
XiU |
| Cascade Au Dessus Des Bras | 3 |
5oA 2iU 2oB |
| Cascade Inversée | X |
XoU |
| Cascade Inversée Au Dessus Des Bras | 3 |
5iA 2iU 2oB |
| Cascade Bras Croisés | X |
XoA XoB |
| Cascade Inversée Bras Croisés | X |
XiA XiB |
| Demi-Douche | X |
XiU XoU |
| Egnever S'nietsnebur (Time Reversed Rubenstein's Revenge) | 3 |
5oB 2iU 2oA 3oB 3iU |
| Funky Mess (Mess USO) | X |
XiU XoB XiA |
| Gillson's Mess (Mess SUS) | X |
XoA XiU XoU |
| Infinite Loop | 3 |
4oU 2oA 4iB 2iU |
| Mess SOS | X |
XoB XiU XoU |
| Mike's Mess | 3 |
5iB 2iU 2oA |
| Mill's Mess | X |
XiU XoA XiB |
| Romeo’s Revenge | 3 |
5iB 2iU 2oA 3iB 3iA |
| Rubenstein's Revenge | 3 |
5iB 2iU 2oA 3iU 3oA |
| Sean's Sequel | 3 |
4iB 2iU 3oA 3iU 3oA |
| Time Reversed Cascade Au Dessus Des Bras | 3 |
2iU 2oB 5iA |
| Time Reversed Cascade Inversée Au Dessus Des Bras | 3 |
2iU 2oB 5oA |
| Time Reversed Funky Mess | X |
XiU XoB XoA |
| Time Reversed Gillson's Mess | X |
XoB XiU XiU |
| Time Reversed Mess SOS | X |
XoA XiU XiU |
| Time Reversed Mill's Mess | X |
XiU XoA XoB |
| Time Reversed Romeo’s Revenge | 3 |
3oA 5oB 2iU 2oA 3oB |
| Windmill (Récupération par Dessus) | X |
XiU XoA |
| Windmill (Récupération par Dessous) | X |
XiU XoB |
Certains noms de figures sont associées à un nombre de balles défini et/ou un siteswap défini; d'autres sont génériques quel que soit le nombre de balles ... c'est le cas de la Cascade, du Mill's Mess ... on peut donc leur adjoindre un nombre X quelconque de balles.
On rappelle qu'à un pattern donné, on peut associer différents siteswaps ainsi qu'un nombre de balles différent. Ainsi si l'on prend l'exemple du Mill's Mess, celui-ci peut être effectué à 3 balles en siteswap 3, 441, 423 ... ou encore à 4 balles, en siteswap 534 par exemple. Pour en déduire directement les diagrammes simplifiés de ces différentes figures, il suffit de prendre la forme simplifiée du Mills Mess (XiU XoA XiB) et d'y adjoindre les différents arrangements de chiffres possibles. On obtient donc ainsi les exemples suivants:
| Mill's Mess 441 | 3 |
4iU 4oA 1iB 1iU 4oA 4iB 4iU 1oA 4iB |
| Mill's Mess 423 | 3 |
4iU 2oA 3iB 3iU 4oA 2iB 2iU 3oA 4iB |
| Mill's Mess 531 | 3 |
5iU 3oA 1iB 1iU 5oA 3iB 3iU 1oA 5iB |
| Mill's Mess 42 | 3 |
4iU 2oA 4iB 2iU 4oA 2iB |
| Mill's Mess 633 | 4 |
6iU 3oA 3iB 3iU 6oA 3iB 3iU 3oA 6iB |
| Mill's Mess 534 | 4 |
5iU 3oA 4iB 3iU 4oA 5iB 4iU 5oA 3iB |
Vous remarquerez que l'on obtient bien 3 Mill's Mess 441 possibles, tout comme 3 Mill's Mess 633 possibles mais 1 seul Mill's Mess 42.
Déduire la symétrie d'un diagramme MMSTD avec siteswap est extrêmement simple. Sans aucune explication vous comprendrez qu'il suffit de transformer les R en l et inversement pour les différents états. Les valeurs du siteswap n'ont aucun impact sur cette symétrie.
Si l'on reprend le diagramme MMSTD de l'Infinite Loop suivant :

Sa symétrie est donc la suivante :

Dans les 2 cas la notation simplifiée est identique puisqu'elle ne prend pas en compte les mains. On a donc 4oU 2oA 4iB 2iU.
5 – Les Inversions dans le temps (Time Reversed)
Comme vous vous en doutez sûrement, si vos diagrammes comportent des siteswaps, les inversions dans le temps de vos diagrammes sont à modifier légérement pour prendre en compte ces différentes valeurs.
Pour la suite nous prendrons la forme simplifiée moins lourde à manipuler. Sans aucune justification (qui peut être retrouvé dans le document de Mike Day cependant), nous présenterons la méthode d'inversion sur quelques exemples.
Le Mill’s Mess 531 et le Time Reversed Mess 531
Le Mill's Mess, présenté dans la vidéo ci-dessus, a pour diagramme :
Ur -o-> Rl -+-> Rr -+-> Ul -o-> Lr -+-> Ll -+-> Ur
En s'aidant du diagramme précédent des passages A, B on obtient la notation simplifiée d'un des 3 Mill’s Mess 531 : 5iB 3iU 1oA.
Les autres s'obtiennent simplement par décalage des lettres. On constate ainsi qu'on a bien 3 Mill's Mess 531 différents : 5iB 3iU 1oA , 1iB 5iU 3oA et 3iB 1iU 5oA
Dans un premier temps on écrit donc le pattern dans l’ordre inverse :
1oA 3iU 5iB
Puis on transforme tous les A en B, les i en o et inversement :
1iB 3oU 5oA
On décale ensuite cycliquement les lettres A, B et U d’un rang vers la gauche. La première lettre revenant à la fin, les o, i, et les chiffres conservant la même position. On obtient donc :
1iU 3oA 5oB
Prenez à present chacun des chiffres et décaler les cycliquement vers la droite de 2 rangs :
3iU 5oA 1oB
Finalement décalez chaque chiffre cycliquement vers la gauche du nombre de rangs égal à leur valeur.
On obtient donc : 3iU 1oA 5oB
que l'on peut comparer avec la vidéo Inversée :
On obtient donc ainsi un Time Reversed Mill's Mess 531.
Le Romeo's Revenge et le Time Reversed Romeo's Revenge
De la vidéo du Romeo’s Revenge on peut en déduire le diagramme MMSTD suivant :
Rl-+->Rr-+->Ul-o->Lr-+->Ll-+->Lr-+->Ll-+->Ur-o->Rl-+->Rr-+->Rl
5 2 2 3 3 5 2 2 3 3 5
On obtient ainsi la notation simplifiée du Romeo’s Revenge : 5iB 2iU 2oA 3iB 3iA
Dans un premier temps on écrit le pattern dans l’ordre inverse :
3iA 3iB 2oA 2iU 5iB
Puis on transforme tous les A en B, les i en o et inversement :
3oB 3oA 2iB 2oU 5oA
On décale ensuite cycliquement les lettres A, B et U d’un rang vers la gauche. La première lettre revenant à la fin, les o, i, et les chiffres conservant la même position. On obtient donc :
3oA 3oB 2iU 2oA 5oB
Prenez à present chacun des chiffres et décaler les cycliquement vers la droite de 2 rangs :
2oA 5oB 3iU 3oA 2oB
Finalement décalez chaque chiffre cycliquement vers la gauche du nombre de rangs égal à leur valeur. Ie un 2 est décalé de 2 rangs, un 3 de 3 rangs …
On obtient donc : 3oA 5oB 2iU 2oA 3oB
que l'on peut comparer avec la vidéo Inversée :
La notation MMSTD complète de cette figure qui est un Time Reversed Romeo's Revenge étant :
Rr-o->Rl-o->Rr-+->Ul-o->Lr-o->Ll-o->Lr-o->Ll-+->Ur-o->Rl-o->Rr
3 5 2 2 3 3 5 2 2 3 3
Voici donc les étapes à effectuer pour inverser une notation simplifiée MMSTD avec siteswap:
2. Puis on transforme tous les A en B, les i en o et inversement. 3. On décale ensuite cycliquement les lettres A, B et U d’un rang vers la gauche. La première lettre revenant à la fin sans toucher aux o, i ni aux chiffres. ==> Jusqu'à présent la démarche est identique à celle que vous avez pu effectuer sur les diagrammes MMSTD sans prise en compte des siteswaps. 4. Prenez à present chacun des chiffres uniquement et décaler les cycliquement vers la droite de 2 rangs. 5. Finalement décalez uniquement chaque chiffre cycliquement vers la gauche du nombre de rangs égal à leur valeur. Ie un 2 est décalé de 2 rangs, un 3 de 3 rangs …
|
V - LES LIMITES DE LA NOTATION MMSTD
1 - L'exemple de l’Infinite Loop
Rappelez-vous du diagramme de l'Infinite Loop de siteswap 42 :

Ce diagramme n'indique en aucun cas, comment sont lancées les balles ni de quelle figure il s'agit. La balle tenue pourrait tout aussi bien être être baladée au-dessus des deux autres.
2 - L'exemple du Yoyo
Même si le Yoyo a pour siteswap 42, on ne va pas s'en occuper ici. On s'intéresse essentiellement à la position des bras.
Vous noterez qu'ici les mains ne sont jamais réellement croisées. On peut cependant considérer que lorsque la balle formant la base du Yoyo est jetée, les bras sont croisés, le bras tenant la balle étant situé au dessus. On obtiendrait donc le diagramme suivant :

Cependant il nous reste à préciser les transitions effectuées par la main tenant la balle du Yoyo. Cette balle est baladée verticalement par la main gauche dans la vidéo précédente. Ici on pourrait encore approximer le mouvement comme un mouvement anti-horaire lors de la montée et horaire lors de la descente. Mais il ne nous ait pas possible de décrire le fait qu'une balle est tenue au dessus d'une autre. La notation MMSTD montre ici ses limites liées au fait qu'elle décrit le mouvement des bras et non pas le mouvement des balles les unes par rapport aux autres. On obtiendrait en effet un diagramme identique si la balle était baladée par la main gauche à gauche de la balle formant la base du Yoyo. De plus même si l'on sait qu'il s'agit d'un 2 (la balle est donc en général tenue), rien ne nous permet de dire que son mouvement de porter est vertical.
3 - Conclusions
Encore une fois, il faut insister sur le fait que de tels diagrammes indiquent uniquement la position des bras ainsi que les échanges. On les qualifie de patterns. A partir d'un pattern, vous pouvez dériver différentes figures avec différents siteswaps. Nous pouvons cependant dès à présent préciser certaines limitations de la notation MMSTD :
- Cette notation ne précise pas les mouvements réels des balles. Ainsi par exemple les lancers en colonnes sont relativement mal décrits.
- Les déplacements des balles ne sont pas suffisement fins si ceux-ci n'amènent pas de changement d'états. C'est le cas du Yoyo, de l'Infinite Loop ...
- Enfin les lancers multiplexes ou synchrones ne sont pas incorporés dans cette notation.
VI - POUR ALLER PLUS LOIN ...
1 – Le diagramme MMSTD et l'algorithmique des graphes
Jusqu'à présent nous avons défini des State Transition Diagrams et indiqué que ces diagrammes ne définissaient pas une figure mais simplement un pattern, c'est à dire un déplacement des bras avec différents échanges. Nous avons également prouvé qu'un tel diagramme pouvait modéliser plusieurs figures totalement distinctes et que pour une meilleure caractérisation de la figure il fallait y adjoindre le siteswap. Tant qu'un siteswap est valide, il est en effet possible de l'appliquer sur un pattern donné.
Avant de poursuivre rappelons cependant quelques définitions relatives à la théorie des graphes en Informatique :
Un chemin : Dans le cas d’un graphe orienté, on peut décrire un chemin par la succession ordonnée des sommets rencontrés partant de l'état initial à l'état terminal.
Un circuit : un circuit est un chemin dont les extrémités coïncident.
Dans le cas d’un graphe non orienté, le chemin s’appelle chaîne et le circuit, cycle.
On peut s'aider de la théorie des graphes en algorithmique pour générer l'ensemble des patterns possibles. Bien que ce problème soit un problème NP-complet (Non-déterministe Polynomial Complet), c'est à dire que la solution demande le parcours complet de ce graphe, on peut cependant étant donné la petitesse du graphe, en fixant des conditions d'arrêt réalistes, en déduire un certain nombre d'éléments. Sans condition, ceci nous amènerait à un problème exponentiel et même infini.
En effet prenons le cas de la simple cascade qui admet le diagramme suivant :
Ur -+-> Ul -+-> Ur ....
Vous constatez bien que cette séquence peut se poursuivre à l'infini. Notre recherche de pattern doit bien être bornée.
Avant tout il nous faut définir la notion de pattern. Nous pourrions définir un pattern comme étant un chemin du graphe, cela engendrait donc des figures avec des états initiaux et des états terminaux. On pourrait ainsi ne les jongler qu'une seule fois. On veut cependant éviter de tels comportements. On veut pouvoir répéter les patterns à l'infini en théorie ;-).
Nous allons donc définir un pattern comme étant un circuit du diagramme. Bien entendu pour entrer dans ce circuit, nous pouvons avoir une séquence préalable qui n'en est pas un. Cependant là n'est pas le sujet. Nous avons donc un début de condition d'arrêt où état initial et état final sont identiques. Cela n'est cependant pas suffisant puisque l'on peut encore avoir des boucles infinies entre ces deux états.
Pour remédier à ce problème nous pouvons fixer les conditions supplémentaires :
- Nombre de passages maximum par Etat : NBPassageEtat. Certains patterns peuvent en effet passer plusieurs fois par le même état. C'est par exemple le cas du pattern du Gillson's Mess en SUS ( Ul -o-> Lr -+-> Ul -o-> Ur -o-> Rl -+-> Ur -o-> Ul)
- Nombre de passages maximum par Transition : NBPassageTransition. Ce paramètre est plus fin que le précédent. On ne cherchera pas à être aussi fin, un état est visuellement plus parlant qu'une transition. Notre exploration se fera donc sans fixer ce paramètre.
- Longueur du pattern : C'est un bon paramètre pour limiter l'exploration du graphe. Il peut même être considéré comme suffisant. Il n'est cependant pas indispensable.
Nos conditions d'arrêt étant données, nous pouvons à présent parcourir le graphe par une stratégie d'exploration en profondeur ou tout simplement par exploration des descendances.
Nous devons également définir un pattern unitaire comme étant un pattern minimal ne passant qu'une seule fois maximum par ses différents états. Un pattern sera alors une combinaison de différents patterns unitaires. Si l'on prend par exemple le cas du Mess SOS, celui-ci est décomposable de la manière suivante :

Pour trouver de nouveau patterns il vous suffit donc d'étendre un pattern à partir d'un état par adjonction d'un nouveau pattern commençant par cet état et ainsi de suite.
2 – Génération de tous les patterns valides en Python
Cet outil baptisé mmstd_gen utilise un algorithme d'exploration des descendances pour touver les patterns valides. Son fonctionnement est simple. Pour un noeud donné, il parcourt la descendance de ce noeud, fils par fils jusqu'à tomber sur une condition d'arrêt. Les conditions d'arrêt paramétrables sont :
- Le nombre de passages maximum par Etat : Vous pouvez fixer cette valeur à :
- 1: Le fait de fixer cette valeur à 1 n'empêche pas la découverte d'un pattern dont noeud terminal et noeud initial sont identiques mais impose simplement de ne passer qu'une seule fois par les autres différents états. Il permet ainsi de générer l'ensemble des patterns unitaires.
- 2 pour autoriser 2 passages par le même état.
- X (X>2) pour autoriser X passages par le même état et même X-2 passages par l'état initial/terminal au sein du pattern. Ainsi par exemple, pour trouver le pattern du Gillson's Mess, vous devrez le fixer à 3 si vous commencez de l'Etat UL ou à 2 simplement si vous commencer de l'état Lr.
- La longueur du pattern : Fixez cette valeur à -1 pour ne pas limiter l'exploration par la longueur du pattern. Dans ce cas là, si votre paramètre du nombre de passages maximum par état est trop important vous risquez de ne pas avoir de condition d'arrêt suffisante; le problème devient infini ;-(.
Cet outil peut-être téléchargé ici et sa documentation est disponible ici.
Ce bout de code est également intégré dans un outil plus récent, en Perl et baptisé
jugglingTB.
Vous pouvez le récupérer ici:
![]() et vous trouverez ici
une documentation succincte concernant
son utilisation.
et vous trouverez ici
une documentation succincte concernant
son utilisation.
3 – L'ensemble des patterns unitaires
Dans la suite nous vous présenterons l'ensemble des patterns unitaires généré à l'aide de cet outil. Certains patterns seront présentés en vidéo pour l'exemple. Vous trouverez des vidéos supplémentaires des patterns les plus connus dans mon article complémentaire lié à la notation S, O, U.
Transitions Unitaires de longueur 2 :
Rr -+-> Rl -+-> Rr [OU] : Cascade Inversée Bras Croisés (Bras Droit au-dessus) [OU]
Rr -+-> Rl -o-> Rr [OU]
Rr -o-> Rl -+-> Rr [OU]
Rr -o-> Rl -o-> Rr [OU] : Cascade Bras Croisés (Bras Droit au-dessus) [OU]
Rr -+-> Ul -o-> Rr [OS] : Windmill (Rattrape Dessous avec MG) [SO]
Ll -+-> Ur -o-> Ll [OS] : Windmill (Rattrape Dessous avec MD) [SO]
Ll -o-> Lr -o-> Ll [OU] : Cascade Bras Croisés (Bras Gauche au-dessus) [OU]
Ll -o-> Lr -+-> Ll [OU]
Ll -+-> Lr -o-> Ll [OU]
Ll -+-> Lr -+-> Ll [OU] : Cascade Inversée Bras Croisés (Bras Gauche au-dessus) [OU]
Ur -+-> Ul -o-> Ur [SS] : Demie-Douche Gauche [SS]
Ur -+-> Ul -+-> Ur [SS] : Cascade [SS]
Ur -o-> Ul -o-> Ur [SS] : Cascade Inversée [SS]
Ur -o-> Ul -+-> Ur [SS] : Demi-Douche Droite [SS]
Ur -o-> Rl -+-> Ur [SU] : Windmill (Rattrape Dessus avec MD) [SU]
Ul -o-> Lr -+-> Ul [SU] : Windmill (Rattrape Dessus avec MG) [SU]
Transitions Unitaire de longueur 4 :
Rr -+-> Rl -+-> Ur -+-> Ul -o-> Rr [OUSS]
Rr -+-> Rl -+-> Ur -o-> Ul -o-> Rr [OUSS]
Rr -o-> Rl -+-> Ur -+-> Ul -o-> Rr [OUSS]
Rr -o-> Rl -+-> Ur -o-> Ul -o-> Rr [OUSS]
Rr -+-> Ul -o-> Ur -o-> Rl -+-> Rr [OSSU]
Rr -+-> Ul -o-> Ur -o-> Rl -o-> Rr [OSSU]
Rr -+-> Ul -+-> Ur -o-> Rl -+-> Rr [OSSU]
Rr -+-> Ul -+-> Ur -o-> Rl -o-> Rr [OSSU]
Ll -+-> Ur -+-> Ul -o-> Lr -o-> Ll [OSSU]
Ll -+-> Ur -+-> Ul -o-> Lr -+-> Ll [OSSU]
Ll -+-> Ur -o-> Ul -o-> Lr -o-> Ll [OSSU]
Ll -+-> Ur -o-> Ul -o-> Lr -+-> Ll [OSSU]
Ll -o-> Lr -+-> Ul -o-> Ur -o-> Ll [OUSS]
Ll -o-> Lr -+-> Ul -+-> Ur -o-> Ll [OUSS]
Ll -+-> Lr -+-> Ul -o-> Ur -o-> Ll [OUSS]
Ll -+-> Lr -+-> Ul -+-> Ur -o-> Ll [OUSS]
Transitions Unitaire de longueur 6 :
Rr -+-> Rl -+-> Ur -o-> Ll -o-> Lr -+-> Ul -o-> Rr [OUSOUS]
Funky Mess [SOUSOU] :
Rr -+-> Rl -+-> Ur -o-> Ll -+-> Lr -+-> Ul -o-> Rr [OUSOUS]
Time Reversed Funky Mess [SOUSOU] :
Rr -o-> Rl -+-> Ur -o-> Ll -o-> Lr -+-> Ul -o-> Rr [OUSOUS]
Rr -o-> Rl -+-> Ur -o-> Ll -+-> Lr -+-> Ul -o-> Rr [OUSOUS]
Rr -+-> Ul -o-> Lr -o-> Ll -+-> Ur -o-> Rl -+-> Rr [OSUOSU]
Time Reversed Mill's Mess [SUOSUO]
Rr -+-> Ul -o-> Lr -o-> Ll -+-> Ur -o-> Rl -o-> Rr [OSUOSU]
Mill's Mess [SUOSUO]
Rr -+-> Ul -o-> Lr -+-> Ll -+-> Ur -o-> Rl -+-> Rr [OSUOSU]
Rr -+-> Ul -o-> Lr -+-> Ll -+-> Ur -o-> Rl -o-> Rr [OSUOSU]
4 – L'ensemble des patterns valides
Voici l'ensemble des patterns générés à l'aide de cet outil pour quelques choix de paramètres :
Nombre de passages max par état |
Longueur Maximum du chemin (-1 : toute longueur) |
Fichiers (Classement par état) |
Fichiers (Suppression des doublons) |
Unitaire (1) |
-1 |
||
2 |
-1 |
||
3 |
8 |
||
3 |
12 |
||
4 |
8 |
||
5 |
8 |
VII - QUELQUES REFERENCES
Il m’est malheureusement impossible de citer ici toutes les sources, certaines sont trop anciennes et il m’est impossible de les retrouver. Néanmoins vous pourrez obtenir plus d’informations :
- Dans le mail originel de Mike Day daté du 17 Février 1995 disponible ici
- Dans la FAQ de Colin Wright.
- ou encore dans les vieux posts de rec.juggling.
- ou bien ceux de jongle.net.
VIII - CONCLUSION
Il ne vous reste plus qu'à utiliser et composer ces différents résultats sur différents siteswaps pour peut-être découvrir de nouvelles figures intéressantes, des transitions entre certaines figures. Vous obtiendrez plus d'exemples si vous vous reportez à mon article concernant l'application de cette notation sur la notation S, O, U.
